Венедикт Ли. Несколько математических задач с решениями
Здесь ряд задач, простых и сложных. Иная - чушь, пустяк - возможно. Но не смотрите так уж кисло, Там есть практичные, со смыслом.
| 1. А решит даже школьник |
| 2. Центр масс? Не тут-то было |
| 3. Евклиду и не снилось |
| 4. Прошла зима, настало лето |
| 5. Маятник или колечко? |
| 6. Вокзалы, вокзалы... |
| 7. Фигаро здесь, Фигаро там |
| 8. Птичий рацион |
Кое-что интересное, по крайней мере для меня. Поскольку я не один на свете любитель математики, то, возможно, еще кто-то сочтет любопытным содержание этой страницы.
В "Грозе над Миром - 2 (Perpetuum mobile)" упоминается задача, которую когда-то решил студент математического факультета Одиссей Гор. К стыду и смущению всей кафедры матанализа, безуспешно бившейся над этой проблемой целый год...
На отрезке E числовой прямой задана функция f(x) ≥ 0, суммируемая со своим логарифмом:
∫E f(x)ln+(f(x))dx = C1 < ∞
На том же отрезке, задана функция g(x) ≥ 0, просто суммируемая:
∫E g(x)dx = C2 < ∞
Доказать, что f(x) суммируема c логарифмом от g(x):
∫E f(x)ln+(g(x))dx < ∞
Здесь ln+ означает срезку логарифма по неотрицательным значениям: ln+(x) = ln(x) при x > 0 и 0 в противном случае. Так же, как обычный логарифм, ln+(x) < x, а для ln+(xy) справедливо очевидное неравенство: ln+(xy) ≤ ln+(x) + ln+(y). Действительно, когда оба сомножителя ≥1, имеем известное школьное правило: логарифм призведения равен сумме логарифмов сомножителей. Если оба ≤1, то будет тривиальное 0 = 0+0. А если один из сомножителей ≤, а другой ≥1, то получим строгое < .
Понятно, что в силу наложенных на обе функции условий, подинтегральное выражение ограничено снизу значением 0. А вот про границу сверху ничего не сказано, и на E обе функции вполне могут обращаться в бесконечность. Надо доказать, что площадь под графиком функции f(x)ln(g(x)) всегда остается конечной.
Замечание. Как может площадь бесконечной фигуры быть конечной?! Для примера: приставьте вертикально к единичнму квадрату сверху его половинку. А к ней сверху так же половинку от половинки. И т.д. Сужающийся столбик уйдет вверх в бесконечность. А его площадь составит: 1 + 1/2 + 1/4 + 1/8 + 1/16 + ... = 2. Так что, интегралы от функций, обращающихся в бесконечность, вполне могут существовать. А могут и не. Смотря какая функция.
Оказывается, что для решения поставленной задачи даже не надо знать, что такое интеграл! Достаточно того, что интеграл от суммы равен сумме интегралов. Гляньте на решение, записанное нахальным студентом на клочке бумаги:
∫f ln+(g) = ∫f ln+(fg/f) ≤ ∫f ln+(f) + ∫f ln+(g/f) =
C1 + ∫f ln+(g/f) < C1 + ∫fg/f = C1 + ∫g = C1 + C2 < ∞
что и требовалось.

Типичный школьный прием - и я бы смогла!
"Цветут поля зеленые! А в них поют влюбленные..." Э-э... не так, начнем заново. В зеленых полях комбайны косят траву. Ее cвозят к агрегату-сушилке, на выходе получается "травяная мука" - концентрат, на корм коровкам, чтобы давали молоко. Полей много, агрегат один.
Куда его поставить, чтобы общие затраты на перевозку к нему сырья с полей были минимальны?
Затраты на перевозку пропорциональны весу груза и расстоянию. Тогда целевая функция выглядит так:
F(z) = Σi r(z,zi)qi --> min
где r(z,zi) - расстояние до i-го поля, а qi - общий вес перевезенного с него груза за сутки. z, zi - координаты на комплексной плоскости.
Вместо агрегата по изготовлению травяной муки, пышущего жаром среди сочных лугов, можете вообразить себе любое перерабатывающее предприятие. Где разместить его среди источников сырья?
Кто-то, взглянув на рисунок, воскликнет: "Рассчитать, как центр масс системы материальных точек! Элементарно!" Отнюдь.
Дадим определение. Функция r(a,b) называется метрикой, если для любых точек а и b выполняются условия:
1) r(a,b) = 0 тогда и только тогда, когда a=b
2) r(a,b) = r(b,a)
3) r(a,b) + r(b,c) ≥ r(a,c)
Условие 3) называют "неравенством треугольника". Из аксиом 1-3 следует также, что метрика неотрицательна: 2r(a,b) = r(a,b) + r(b,a) ≥ r(a,a) = 0.
Теорема. Обозначим: Q = Σi qi. Если qk ≥ Q/2, то точка zk есть решение задачи.
Доказательство. F(zk) = Σi≠k r(z,zi)qi ≤ Σi≠k (r(zk,z)+r(z,zi))qi =
r(zk,z)Σi≠kqi + Σi≠k r(z,zi)qi ≤ r(z,zk)qk + Σi≠k r(z,zi)qi = F(z) для любого z ≠ zk
Обратите внимание, что результат не зависит от метрики. Достаточно того, что мощность источника сырья больше, чем всех остальных, вместе взятых. Там и следует располагать центр переработки.
Что, кстати, доказывает неправильность гипотезы "центра масс" для решения нашей задачи. Ведь для системы материальных точек с ненулевыми массами центр масс никак не может совпасть с одной из этих точек!
Решение для евклидовой метрики. Пусть z - точка на комплексной плоскости. Вещественную и мнимую координаты будем традиционно именовать x, y. Целевая функция:
F(x,y) = Σi((x-xi)2+(y-yi)2)1/2qi --> min
Прошу прощения, за то, что квадратный корень обозначаю, как степень 1/2. Возможности веб-страниц не позволяют набирать формулы более красиво.
Дифференцируя, независимо, по x и y, и приравнивая обе производные к 0, получаем громоздкие формулы для последовательных приближений. Сходимость зато - очень быстрая.
x = Σixiqi/((x-xi)2+(y-yi)2)1/2 / Σiqi/((x-xi)2+(y-yi)2)1/2
y = Σiyiqi/((x-xi)2+(y-yi)2)1/2 / Σiqi/((x-xi)2+(y-yi)2)1/2
Можно и короче записать, введя обозначение ri = ((x-xi)2+(y-yi)2)1/2
x = Σixiqi/ri / Σiqi/ri
y = Σiyiqi/ri / Σiqi/ri
Вопрос: что брать в качестве начального, т.н. "нулевого" приближения? Да что угодно. Например, бесконечно удаленную точку. Тогда все расстояния ri от нее до пунктов поставки будут одинаковыми бесконечностями, обозначим их R. И увидим, что в числителях и знаменателях формул для x, y они сократятся. Получится:
x = Σixiqi / Σiqi
y = Σiyiqi / Σiqi
А это и есть формула для центра масс! Т.о. центр масс - хотя и неточное, но вполне уже правдоподобное первое приближение.
Решение для Манхеттенской метрики. Расстояние определяется, как сумма разностей координат по x и y. И целевая функция имеет вид F(x,y) = Σi(|x-xi|+|y-yi|)qi
Что равносильно езде по взаимно перпендикулярным улицам крупного современного города. Прямо, направо, налево, приехали. Это вам не чисто поле, напролом не попрешь.
Снова дифференцируем по х и у, приравнивая производные к 0, и помня, что d|x|/dx = sign(x), где sign(x) = 1 при x > 0 и -1 при x <0. Выкрики из зала о том, что здесь в нуле производная не существует, пропускаем мимо ушей. Получаем интересные равенства для x и y, с двухэтажными уровнями индексации.
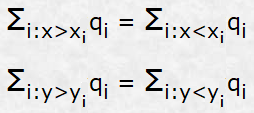
Парадокс, да? В общем случае эти равенства практически никогда не выполняются, левая часть может быть только < или > правой. Таким образом, оптимальной координатой x (или y) будет та из координат xi (или yi) в которой соответствующее неравенство меняет знак. На карте эту точку легко найти, двигая вертикально поставленную линейку вдоль оси X и подсчитывая суммарные мощности поставщиков слева и справа. Аналогично, горизонтально повернутую линейку двигаем вдоль оси Y и считаем мощности поставщиков снизу и сверху. Вот тестовый пример. Решение по гипотезе "центра масс": (1.75, 1.15). На самом деле, по евклидовой метрике будет: (1.0784, 1.0106); по манхеттенской: (2, 1).
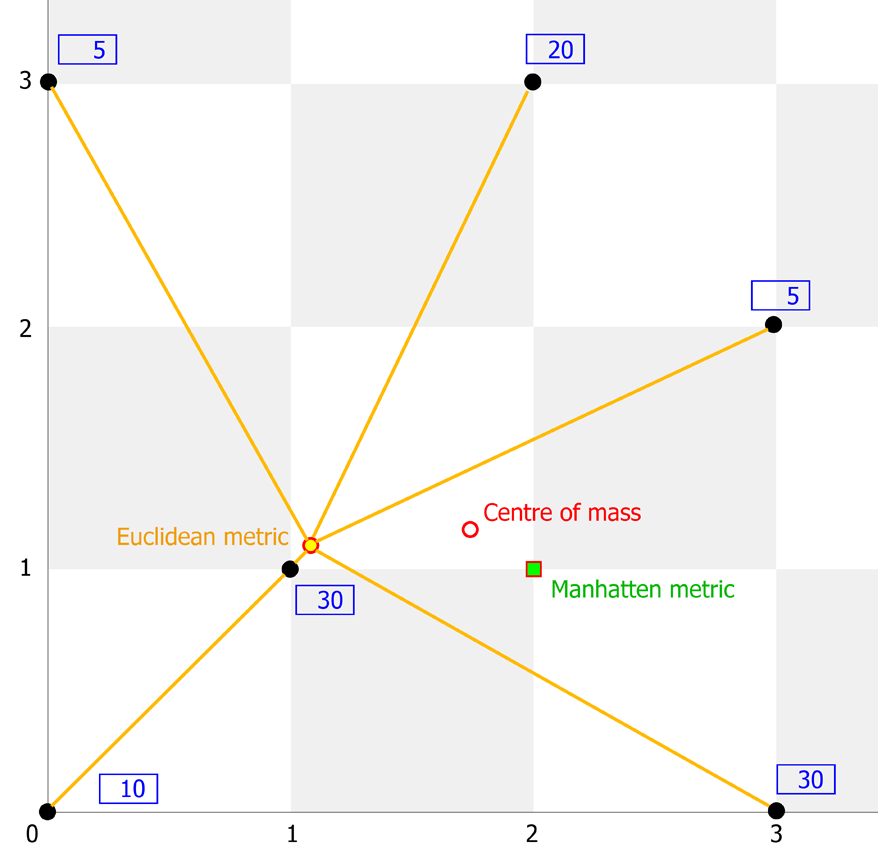
Питон-скрипт с примером расчета по евклидовой метрике находится здесь.
В "Грозе над Миром - 3. Nовое Vремя" сын фермера Джиль как-то умудрился успешно скрестить... теорию чисел с сельским хозяйством! В чем же состоял его секрет?
Уборочно-транспортное звено - самая распространенная форма труда при уборке сельхозкультур. Оно состоит из определенного количества комбайнов (m), и транспортных средств (n). Важно определить такое соотношение этих машин, при котором обеспечивается ритмичность процесса уборки и вывозки урожая.
Условие ритмичности уборочно-транспортного процесса состоит в равенстве суммарной часовой производительности комбайнов (Wк) и транспортных средств (Wтр), входящих в уборочно-транспортное звено:
Wкm = Wтрn
или, что то же самое:
Wтр / Wк = m / n
Вот тут мы и приплыли... Слева стоит отношение двух вещественных чисел, а справа рациональная дробь, и такое равенство представить себе затруднительно. Однако, попробуем.
Пусть Wтр = 3.22 т/ч, Wк = 5.57 т/ч. Тогда 3.22 / 5.57 = 322 / 557. Такое соотношение комбайнов (322) и транспортных средств (557) - нереально.
На практике, это как-нибудь округляют, и все дела. Ну, там 1/2 или 2/3 и т.п. Насколько не угадали, настолько и будут простаивать избыточные комбайны или транспортные средства. В общем, без метода проб и ошибок не обойтись, да?
Однако, существует способ найти наилучшее приближение, (при заданном ограничении на число комбайнов или транспортных средств) без длительных проб и проверок. Он заключается в превращении отношения Wтр / Wк в ту самую "нереальную" рациональную дробь, затем в разложении ее в цепную дробь. Из полученной цепной дроби получаем ряд "подходящих" дробей к данной цепной дроби.
Метод разложения правильной рациональной дроби в цепную дробь открыт примерно 2000 лет назад и называется "алгоритм Евклида".
Пусть p/q - правильная рациональная дробь, т.е. p < q. Преобразуем ее так:
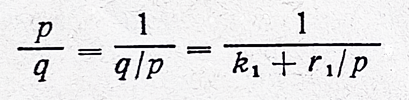
где k1 - целая часть от неправильной дроби q/p; r1 - остаток от q на p, следовательно r1 < p, а дробь r1/p - правильная. Повторим с нею тот же прием:
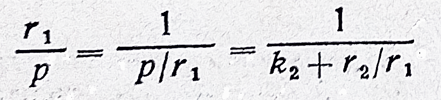
Дробь r2/r1 - снова правильная, и опять применяем указанный прием. Когда последний из остатков станет равным 0, процесс заканчивается:
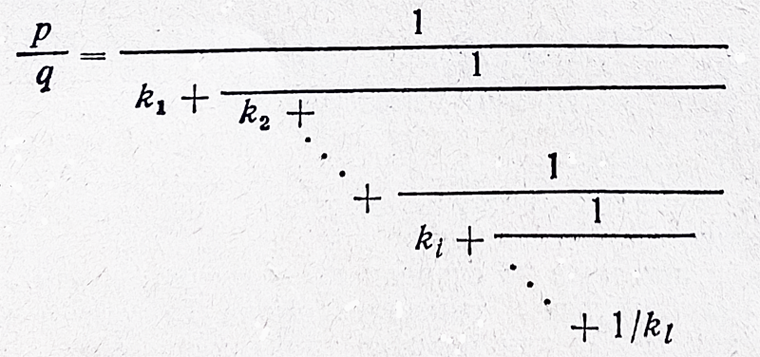
Сокращенно это можно записать, как p/q = [ k1, k2, ... ki, ... kl ].
Разложив правильную рациональную дробь в цепную, составляем для нее подходящие дроби: [k1] = 1/k1, [k1,k2] = 1/(k1+1/k2) и т.д. Каждая подходящая дробь ближе к p/q, чем предыдущая. Для пояснения рассмотрим наш изначальный пример.

или, в сокращенном виде Wтр / Wк = [ 1, 1, 2, 1, 2, 2, 1, 8 ].
Из полученной дроби составляем ряд подходящих дробей: 1/1, 1/2, 3/5, 4/7, 11/19, 26/45, 37/64.
В качестве величины m/n принимается та из подходящих дробей, которая удовлетворяет принятому ограничению на числитель или знаменатель, и при том, обеспечивает требуемую степень приближения к Wтр/Wк
В ряду подходящих дробей первая всегда соответствует некоторому избытку комбайнов, и следовательно, указывает на их простои. Вторая - на простои транспортных средств. Третья - снова на простои комбайнов, и т.д. Доля времени, приходящаяся на простои комбайнов или транспортных средств, никогда не превышает величины 1/mn.
Для пояснения, опять вернемся к нашему примеру. Если в распоряжении хозяйства не более 6 транспортных единиц, то наилучшим вариантом будет m/n = 3/5, то есть 3 комбайна и 5 транспортных средств. Поскольку - это третья дробь в ряду подходящих, то она соответствует простою комбайнов, доля которого не превысит 1/15 ≈ 6.7% рабочего времени.
Если ограничено число комбайнов, например, не более 6, то наилучшим соотношением будет m/n = 4/7. Это четвертая дробь в ряду, следовательно, транспортные средства будут простаивать 1/28 ≈ 3.6% рабочего времени.

Умираю от смеха, помогите... Представила Евклида за рулем грузовика!
4. Прошла зима, настало лето
(сезонные колебания потребности в транспорте - где оптимум?)
5. Маятник или колечко?
(маятниковые и кольцевые маршруты)
6. Вокзалы, вокзалы...
(сколько их и где должно быть?)
7. Фигаро здесь, Фигаро там
(развозочные маршруты)
8. Птичий рацион
(классика линейного программирования)